Credit/Quelle: WBI GmbH
1 Veranlassung
Ein sicherer und wirtschaftlicher Entwurf von Hohlraumbauten in klüftigem Fels setzt eine realitätsnahe Berücksichtigung des Zusammenwirkens von Baugrund und Bauwerk voraus.
Das zur Bemessung von Stahlbetontübbingen immer noch angewendete Bettungsmodulverfahren, bei dem eine angenommene Last auf einen elastisch gebetteten Tübbingring wirkt, erfüllt diese Voraussetzung weder für den fertigen Zustand, noch können damit die wichtigen Bauzustände vom Einbau der Tübbinge bis zum Endzustand zutreffend beschrieben werden. Selbst bei nach der Spritzbetonbauweise aufgefahrenen Tunneln findet man vereinzelt noch Standsicherheitsnachweise, die diesem Ansatz folgen.
Auch die immer wieder angepriesenen Klassifizierungsmethoden erfüllen die an die Planung zu stellenden Anforderungen nicht. Mit ihnen wird – wie beispielsweise beim Q-System – versucht, das komplexe Gebirgsverhalten anhand eines Produktansatzes mit Daten zum Trennflächengefüge und einem sogenannten stress reduction factor mit Hilfe einer Kennziffer zu erfassen. Mit dieser Kennziffer kann man dann die für einen Tunnel erforderlichen Sicherungsmaßnahmen aus verfügbaren Diagrammen ablesen [1]. Dass diese Methode zu nicht standsicheren oder aber zu unwirtschaftlichen Lösungen führen kann und somit wenig zuverlässig ist, wurde bereits in [2, 3] gezeigt und wird im folgenden Artikel kurz aufgegriffen.
Für Standsicherheitsnachweise zumindest auf den ersten Blick geeignet ist sicherlich die Vorgehensweise von Hoek–Brown [1, 4]. Hoek-Brown stellen eine Abbildung zur Verfügung, mit deren Hilfe man anhand einer qualitativ-quantitativen Beschreibung des Trennflächengefüges eines Felses den sogenannten geological strength index (GSI) bestimmen kann. Mit diesem Wert kann man bei Kenntnis der einaxialen Festigkeit des jeweiligen Gesteins dann eine nichtlineare Beziehung zwischen der größten und kleinsten Hauptnormalspannung für den Bruchzustand und damit das Bruchkriterium für den jeweiligen Fels herleiten. Näherungsweise kann man nach Hoek-Brown auch das Mohr Coulomb‘sche Bruchkriterium anwenden und einen äquivalenten Reibungswinkel sowie eine Kohäsion für den klüftigen Fels errechnen. Weiterhin wird eine Beziehung für die Ermittlung des E-Moduls des Felses mit Hilfe des GSI angegeben.
Leider geht dieser Ansatz von isotropem elastischen Verhalten und von isotroper Festigkeit aus und vernachlässigt die Anisotropie von klüftigem Fels, die man in den meisten Fällen weder im elastischen Bereich noch hinsichtlich der Festigkeit außer Acht lassen darf. Es kommt noch hinzu, dass die Anwender dieser Methode in vielen Fällen zu geringe Scherparameter für das anstehende Gebirge ableiten und damit den anstehenden Fels in der Planung wie einen Boden behandeln. Auf diese Weise kann es zu sehr teuren Lösungen kommen, wie im vorliegenden Artikel anhand eines Beispiels gezeigt wird.
Die Autoren folgen bei Ihren Planungen deshalb schon seit vielen Jahren mit Erfolg dem Anisotropic Jointed Rock Modell (AJRM) und dem darauf aufbauenden Verfahren für Standsicherheitsnachweise und zur Prognose der Verschiebungen. Die Erfahrungen an vielen ausgeführten Tunnel- und Felsbauwerken und die dabei durchgeführten Beobachtungen und Messungen haben gezeigt, wie erfolgreich dieses Entwurfskonzept ist.
Der vorliegende Artikel soll dies an einigen ausgewählten Beispielen zeigen. Er wendet sich vor allem an die Bauherrenschaft, weil diese einerseits die Kosten für unwirtschaftliche Lösungen tragen muss und andererseits einen großen Einfluss auf Art und Umfang von Voruntersuchungen und auf den Entwurf hat.
Der Artikel ist in zwei Teilen abgefasst. In dem vorliegenden Teil werden die Themen felsmechanisches Modell und zugehörige Fallbeispiele behandelt. In dem zweiten Teil des Artikels wird auf das felshydraulische Modell, zugehörige Fallbeispiele sowie die Ermittlung der felsmechanischen und felshydraulischen Kennwerte eingegangen. In der Gesamtheit werden damit die Grundlagen und Anwendungsbeispiele einerseits für die statische Betrachtung, Bemessung und Planung von Bauwerken im Fels und andererseits für hydrogeologische Betrachtungen (Grundwassermodelle) erläutert, wobei die aus der Sickerströmung resultierenden Kräfte selbstverständlich auch im statischen Nachweis zu berücksichtigen sind.
Die Autoren möchten ausdrücklich zur fachlichen Diskussion anregen und hoffen, dass auch in der Forschung weiter an der Verfeinerung der AJRM-Methode gearbeitet wird.
2 Felsmechanisches Modell
Fels ist in einer Vielzahl von Fällen gekennzeichnet durch verschiedene Komponenten, wie Gestein, Trennflächen (Klüfte/Schichtfugen/Schieferung), Störungen, Falten. Dies gilt im besonderen Maße für Sedimentgesteine und metamorphe Gesteine. Diese Felsarten sind in der Regel anisotrop im Hinblick auf die Festigkeit und häufig auch im Hinblick auf die Verformbarkeit. Dies muss bei felsstatischen Berechnungen berücksichtigt werden. Bei der Bemessung von Holzleimbindern würde schließlich auch kein Ingenieur die Anisotropie des Baustoffs vernachlässigen.
Grundlage für eine wirklichkeitsnahe Erfassung des Festigkeits- und Verformungsverhaltens von Fels ist die Erarbeitung eines zutreffenden felsmechanischen Modells beruhend auf Gefügemodellen und Kennwerten [5, 6]. Für Beanspruchungen unterhalb der Festigkeit kann man bei den meisten Felsarten näherungsweise von linear-elastischem Verhalten ausgehen. Sedimentgesteine, Tonschiefer und auch Gneise verhalten sich aber im elastischen Bereich nicht immer isotrop. Vielmehr ist die Zusammendrückbarkeit senkrecht zur Schichtung oder Schieferung häufig größer als parallel dazu. Diese Eigenschaft darf in vielen Fällen nicht vernachlässigt werden und kann durch die Annahme transversaler Isotropie in guter Näherung beschrieben werden.
Beispielhaft zeigt Bild 1 eine Wechsellagerung von Kalksandsteinen und Tonsteinen aus dem Lias α des Unteren Jura. Der Sandstein ist durch ein regelloses Korngefüge des Gesteins sowie schichtparallele, horizontale Bankungsfugen und steil stehende Kluftscharen gekennzeichnet. Er weist bis zum Erreichen der Festigkeit ein näherungsweise isotropes Verformungsverhalten auf, welches durch den E-Modul und die Querkontraktionszahl beschrieben werden kann. Dahingegen besitzen die Tonsteine eine planare Kornstruktur sowie schichtparallele, horizontale Bankungsfugen und weniger ausgeprägte vertikale Klüfte. Dies führt zu einer Anisotropie des Verformungsverhaltens: die Tonsteine sind in vertikaler Richtung stärker verformbar als in horizontaler, schichtparalleler Richtung. Die näherungsweise transversale Isotropie des Verformungsverhaltens lässt sich durch 5 elastische Konstanten beschreiben (Bild 1): die E-Moduln parallel und senkrecht zur Schichtung E1 und E2, zwei Poisson‘sche Zahlen ν1 und ν2 und den Schubmodul G2 [5, 6].
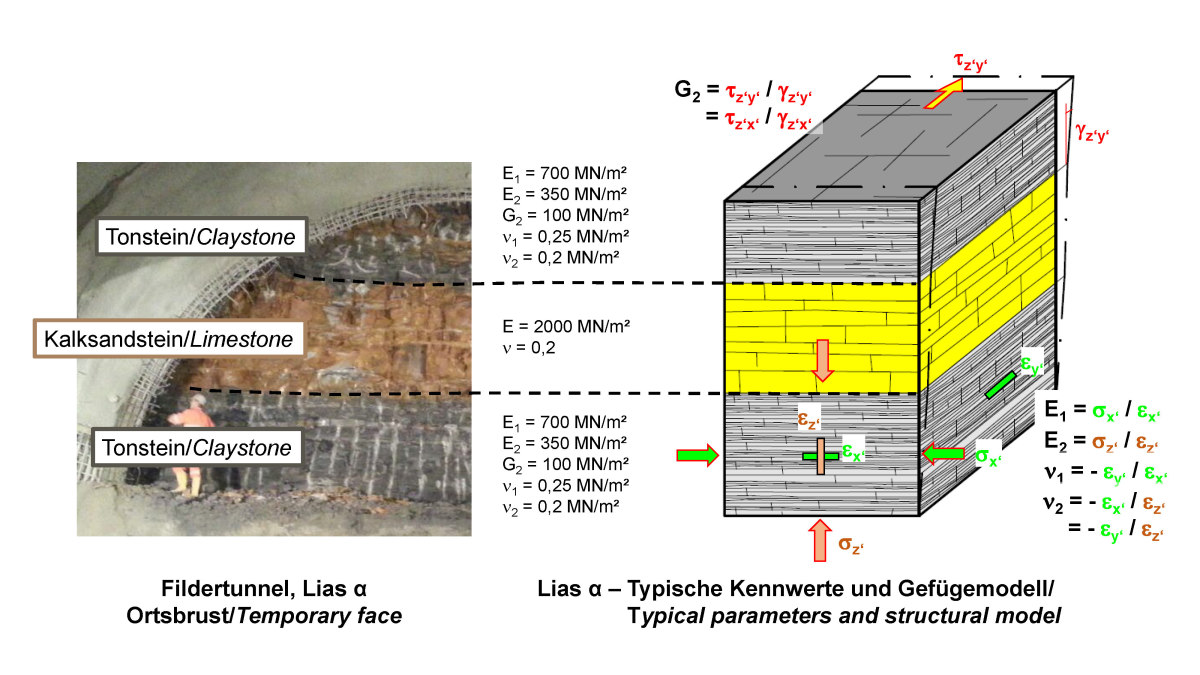 1 | Lias α – Foto Ortsbrust, Gefügemodell und elastische Konstanten als Teil eines felsmechanischen Modells
1 | Lias α – Foto Ortsbrust, Gefügemodell und elastische Konstanten als Teil eines felsmechanischen Modells
Credit/Quelle: WBI GmbH
1 | Lias α – Foto Ortsbrust, Gefügemodell und elastische Konstanten als Teil eines felsmechanischen Modells
Credit/Quelle: WBI GmbH
Ein weiteres Beispiel für die Beschreibung des elastischen Verhaltens von klüftigem Fels zeigt Bild 2. Es handelt sich um eine Wechsellagerung von Sand- und Schluffsteinen der Waichecheng Serie. Hier liegen zwischen den Sand- und Schluffsteinen schichtparallele Scherzonen vor. Die Scherzonen weisen eine deutlich höhere Verformbarkeit und geringere Festigkeit auf als die umgebenden Felspakete (Sand-/Schluffstein). Dies führt zu einem transversal-isotropen Verformungsverhaltens des Felses. Die zur Beschreibung dieses Verhaltens erforderlichen elastischen Konstanten lassen sich vergleichsweise einfach aus den elastischen Konstanten der einzelnen Komponenten (Fels/Trennflächenfüllung) rechnerisch ermitteln. Schematisch ist dies in Bild 2 auf der rechten Seite dargestellt. Die Einzelheiten nebst Formeln sind in [6] erläutert.
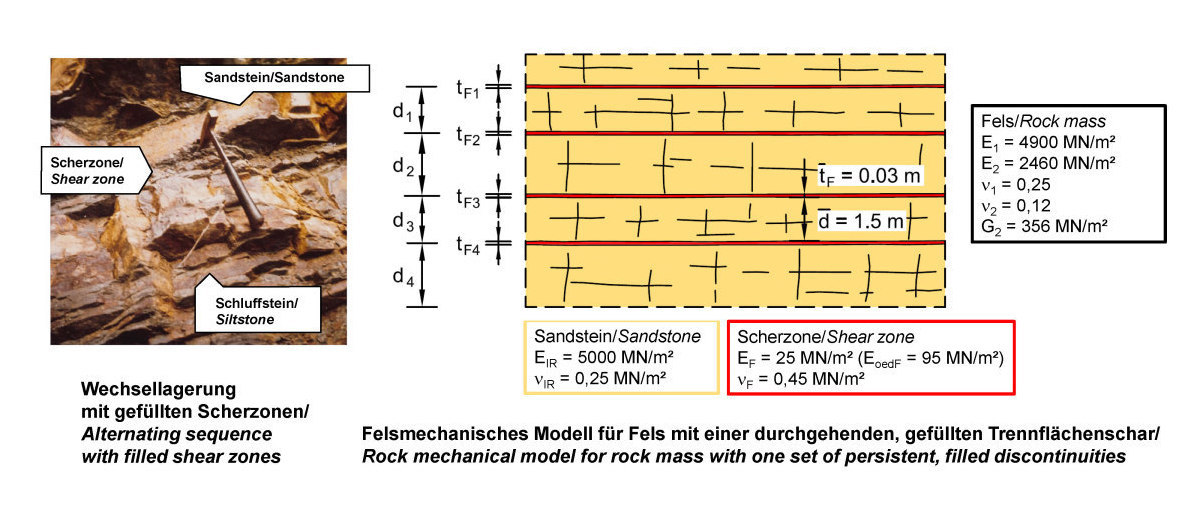 2 | Fels mit 1 Schar durchgehender, gefüllter Trennflächen – Foto und Bestimmung der elastischen Konstanten [6]
2 | Fels mit 1 Schar durchgehender, gefüllter Trennflächen – Foto und Bestimmung der elastischen Konstanten [6]
Credit/Quelle: [6]
2 | Fels mit 1 Schar durchgehender, gefüllter Trennflächen – Foto und Bestimmung der elastischen Konstanten [6]
Credit/Quelle: [6]
Die Festigkeit des unzerklüfteten Gesteins ist nur in Ausnahmefällen von Bedeutung für das mechanische Verhalten. In der Regel stehen aber für die Beschreibung der Festigkeit des Gesteins Ergebnisse einaxialer Druckversuche zur Verfügung. Bei Annahme eines Reibungswinkels für das Gestein φIR, kann man nach dem Mohr-Coulomb‘schen Gesetz die Kohäsion cIR ermitteln, wie in Bild 3 für das Beispiel eines Buntsandsteins dargestellt.
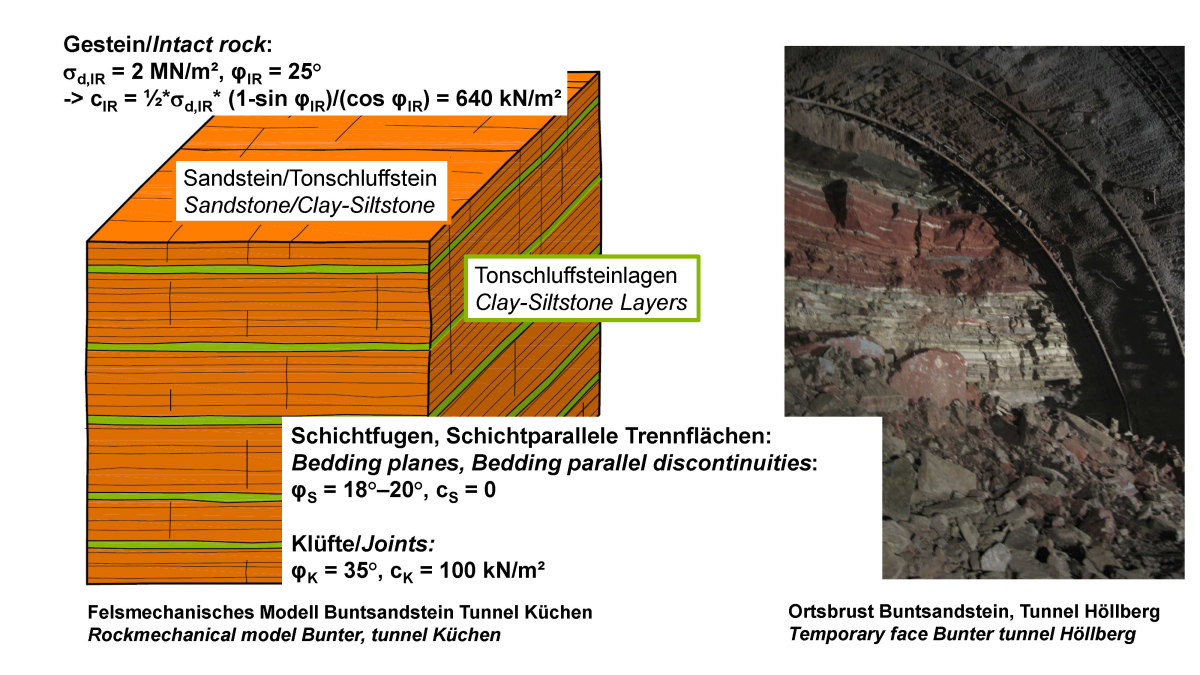 3 | Buntsandstein – Foto Ortsbrust, Gefügemodell und Festigkeitseigenschaften als Teil des felsmechanischen Modells
3 | Buntsandstein – Foto Ortsbrust, Gefügemodell und Festigkeitseigenschaften als Teil des felsmechanischen Modells
Credit/Quelle: WBI GmbH
3 | Buntsandstein – Foto Ortsbrust, Gefügemodell und Festigkeitseigenschaften als Teil des felsmechanischen Modells
Credit/Quelle: WBI GmbH
Maßgeblich für die Standsicherheit sind aber die Scherfestigkeiten auf den Trennflächen, die in der Praxis im felsmechanischen Modell ebenfalls durch einen Reibungswinkel und eine Kohäsion beschrieben werden können, auch wenn nicht-lineare Ansätze für die Beschreibung des Festigkeits- und Schubspannungs-Scherverschiebungsverhaltens zur Verfügung stehen. Wie das Beispiel des Buntsandsteins in Bild 3 zeigt, weisen die Trennflächen eine gegenüber der Gesteinsfestigkeit erheblich reduzierte Scherfestigkeit auf. Dies gilt im besonderen Maße für die schichtparallelen Bankungsfugen. Dies führt zu einer Anisotropie in der Festigkeit des Felses.
Eine Zugfestigkeit wird in geklüftetem Fels in der Regel nicht in Ansatz gebracht. Weitere Beispiele für entsprechende felsmechanische Modelle von klüftigem Fels finden sich in [6]. Diese können als Grundlage für erste Untersuchungen herangezogen werden, wenn noch keine Ergebnisse von projektspezifischen Erkundungen vorliegen.
Bei der Modellierung von Fels im sogenannten homogenen Modell wird davon ausgegangen, dass die zu berücksichtigenden Trennflächen an jedem Punkt des Modells auftreten („verschmierte Modellierung“). Dies erlaubt die Berücksichtigung verschiedener Trennflächenscharen und damit der Festigkeits- und Verformbarkeits-Anisotropie mit vergleichsweise geringem Aufwand. Diese Vorgehensweise führt dann zu verlässlichen Ergebnissen, wenn die Abmessungen des jeweils betrachteten Bauwerks groß sind im Vergleich zum Trennflächenabstand (s < ~ 1/8 bis 1/10 *D, siehe Bild 4, links [6]). Diese Voraussetzung ist für Klüfte, Schichtfugen, Schieferungsfugen in Sediment- und metamorphen Gesteinen und Felsbauwerke üblicher Abmessungen in der Regel erfüllt. Eine diskrete Modellierung wird dann erforderlich, wenn die Trennflächenabstände groß sind im Vergleich zu den Bauwerksabmessungen (vgl. Bild 4, rechts). Dies kann z.B. für Störungen zutreffen. Bei Erfordernis ist es daher möglich, das homogene Modell mit einer diskreten Modellierung einzelner Strukturen, wie z. B. Störungen, zu kombinieren [6].
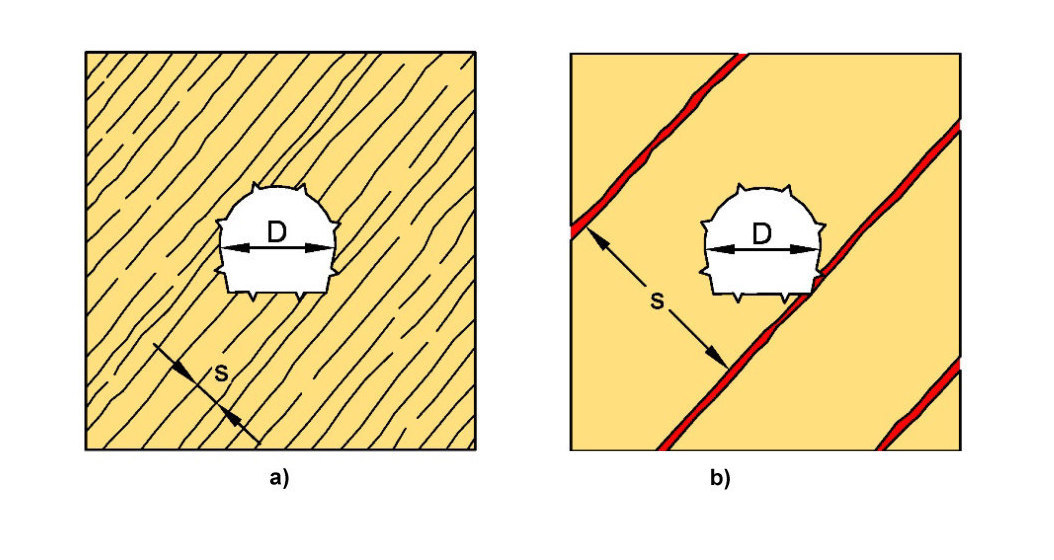 4 | Trennflächenabstand im Vergleich zu Bauwerksab-
4 | Trennflächenabstand im Vergleich zu Bauwerksab-
messungen
a) Berücksichtigung im homogenen Modell vs. b) diskrete Modellierung [6]
Credit/Quelle: [6]
4 | Trennflächenabstand im Vergleich zu Bauwerksab-
messungen
a) Berücksichtigung im homogenen Modell vs. b) diskrete Modellierung [6]
Credit/Quelle: [6]
Die Notwendigkeit der diskreten Berücksichtigung einzelner Schichten bzw. Diskontinuitäten ist sowohl hinsichtlich des elastischen Verhaltens als auch hinsichtlich der Festigkeitseigenschaften für jedes Projekt zu untersuchen.
3 Fallbeispiele 3.1 Tonsteine des Unteren Jura (Lias α), Tunnel Österfeld
In den Tonsteinen des unteren Jura wurden und werden in Deutschland eine Vielzahl von Tunneln gebaut. Für jedes der seit mehr als 40 Jahren von den Autoren betreuten Projekte wurden die Ergebnisse der durchgeführten Erkundungen ausgewertet, und die beim Bau erhaltenen Messergebnisse wurden mit den Prognosen verglichen. Somit steht eine umfangreiche Datenbasis zur Verfügung, die es ermöglicht, das Verhalten des Felses mit sehr hoher Prognosesicherheit zu beschreiben. Das zeigt sich auch bei den aktuell aufgefahrenen Tunneln für den Anschluss des Stuttgarter Flughafens an die Neubaustrecke von Stuttgart nach Ulm und dem Bau der unterirdischen Station über die an anderer Stelle detailliert berichtet wird. Für den vorliegenden Beitrag wird auf einen Straßentunnel zurückgegriffen, der vor etwa 25 Jahren nach der AJRM-Methode erfolgreich geplant und ausgeführt wurde und noch heute in Betrieb ist. Zu einem späteren Zeitpunkt wurde zum Zweck des Vergleichs für diesen Tunnel ein Planungskonzept auf der Grundlage von Klassifizierungsmethoden erstellt [2].
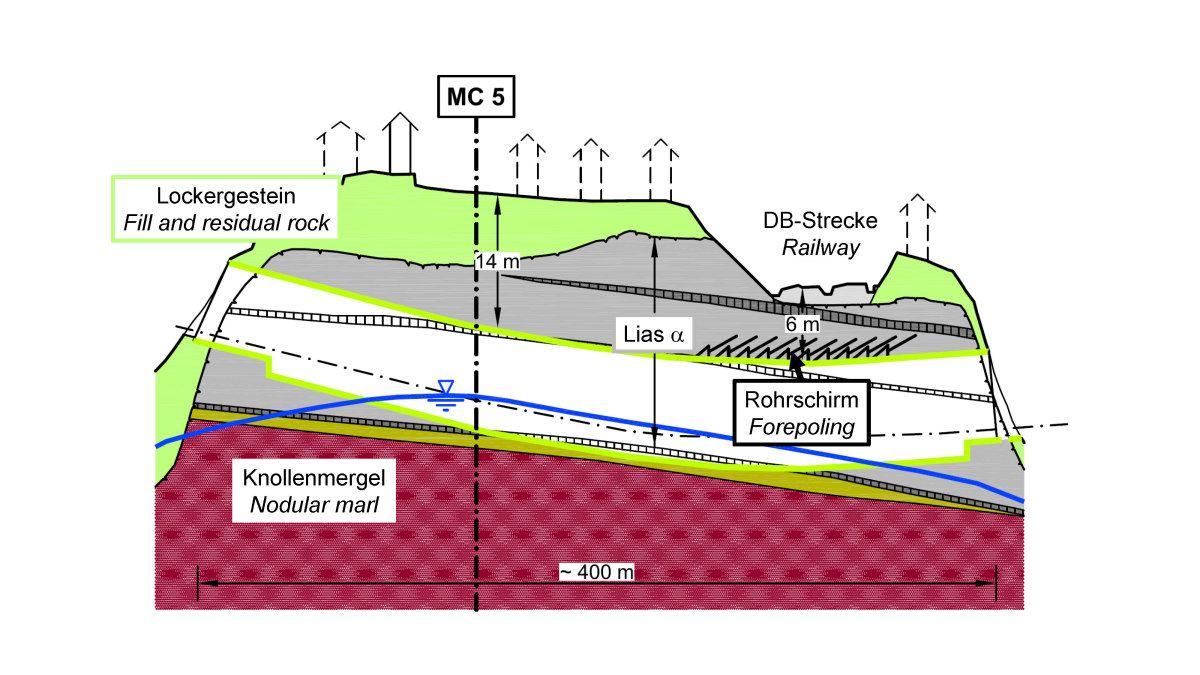 5 | Ortsumfahrung Vaihingen (Stuttgart), Österfeldtunnel, Geologischer Längsschnitt [7]
5 | Ortsumfahrung Vaihingen (Stuttgart), Österfeldtunnel, Geologischer Längsschnitt [7]
Credit/Quelle: WBI GmbH
5 | Ortsumfahrung Vaihingen (Stuttgart), Österfeldtunnel, Geologischer Längsschnitt [7]
Credit/Quelle: WBI GmbH
Der etwa 400 m lange Straßentunnel Österfeld wurde als Teil der Ostumfahrung Vaihingen in Stuttgart aufgefahren (Bild 5). Er kommt nahezu vollständig in den Tonsteinen des Lias α zu liegen, deren felsmechanisches Modell in Bild 1 dargestellt ist. Wie bereits erwähnt, weisen die Tonsteine eine ausgeprägte Anisotropie der Verformbarkeit (E1 ~ 2 * E2, Bild 1) auf. Aus anderen Projekten in der näheren Umgebung war zum Zeitpunkt der Planung bekannt, dass in den Tonsteinen des Lias α im Projektgebiet erhöhte Horizontalspannungen zu erwarten sind, die aus einer geologischen Vorbelastung resultieren. In-situ Spannungsmessungen hatten zusätzliche Horizontalspannungen in der Größenordnung von ΔσH = 0,2–1,9 MPa ausgewiesen. Die Standsicherheitsberechnungen wurden auf der Grundlage eines felsmechanischen Modells unter Berücksichtigung der Anisotropie der Verformbarkeit sowie der erhöhten Horizontalspannungen nach der FE-Methode ausgeführt (AJRM, vgl. felsmechanisches Modell in Bild 1). Hierauf fußend wurden Ausbruch und Sicherung sowie die Auskleidung des Tunnels geplant. Der Tunnel wurde im Maulprofil mit einer lichten Breite von 11,2 m und einer lichten Höhe von 9,7 m aufgefahren (Bild 6, links). Aus baubetrieblichen Gründen wurde ein Vortrieb mit vorauseilender Kalotte vorgesehen, die zur Minimierung der Senkungen mit geschlossener Sohle ausgeführt wurde. Alternativ wäre auch ein Vollausbruch mit abgetreppter Ortsbrust möglich gewesen [8]. Der Ausbruchquerschnitt wurde mit einer 25–30 cm dicken Spritzbetonschale und einer radialen Ankerung gesichert (Bild 6, links).
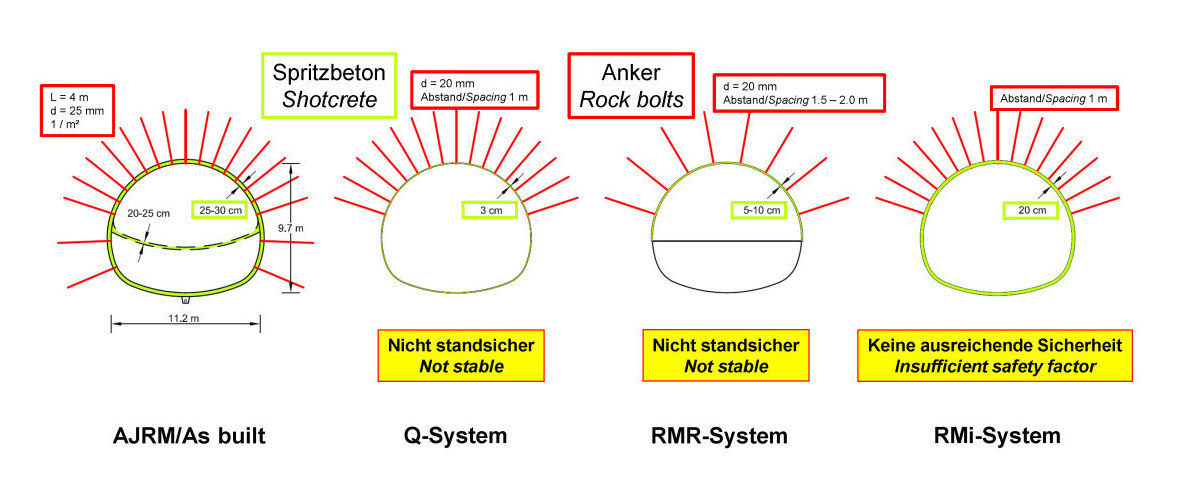 6 | Österfeldtunnel, Ausbruch und Sicherung auf Basis AJRM im Vergleich mit Sicherungsempfehlungen nach Klassifizierungssystemen Q, RMR und RMi [2, 3]
6 | Österfeldtunnel, Ausbruch und Sicherung auf Basis AJRM im Vergleich mit Sicherungsempfehlungen nach Klassifizierungssystemen Q, RMR und RMi [2, 3]
Credit/Quelle: [3]
6 | Österfeldtunnel, Ausbruch und Sicherung auf Basis AJRM im Vergleich mit Sicherungsempfehlungen nach Klassifizierungssystemen Q, RMR und RMi [2, 3]
Credit/Quelle: [3]
Der Vortrieb wurde mit einem umfassenden Messprogramm begleitet. Die Messergebnisse wurden mit den rechnerischen Prognosen verglichen. Bild 7 zeigt den Vergleich von Mess- und Berechnungsergebnissen für die Annahme ΔσH = 1 MPa. Es zeigt sich eine sehr gute Übereinstimmung.
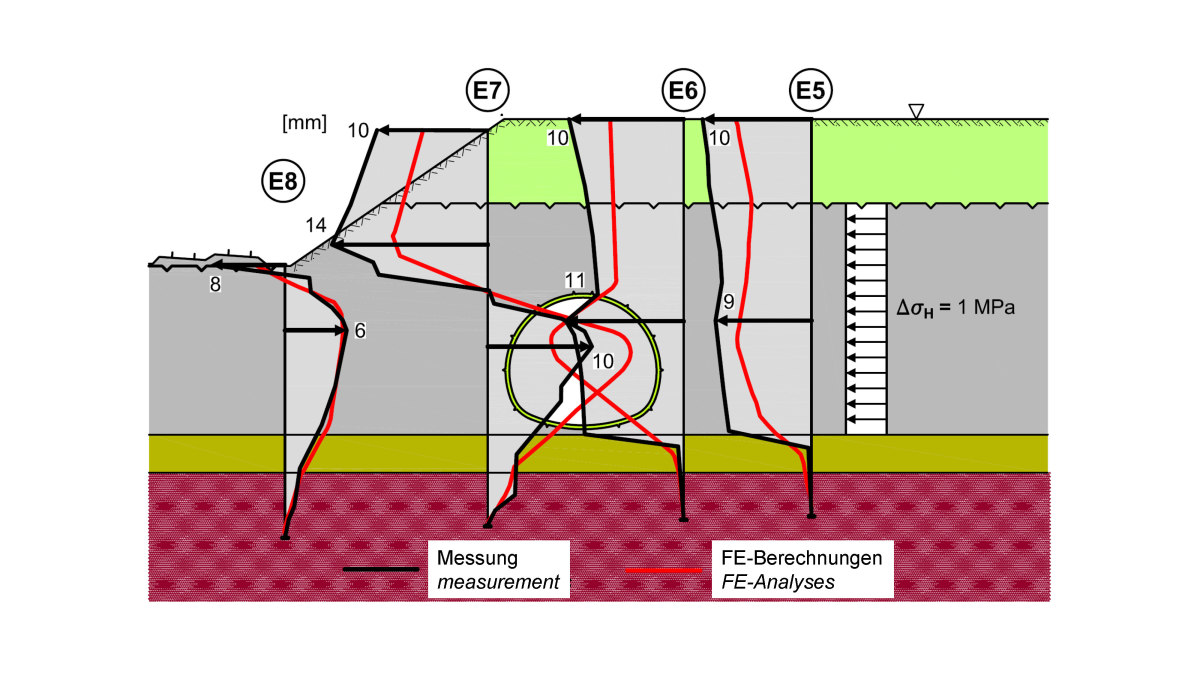 7 | Österfeldtunnel, Horizontalverschiebungen, Vergleich Rechnung – Messung [7]
7 | Österfeldtunnel, Horizontalverschiebungen, Vergleich Rechnung – Messung [7]
Credit/Quelle: WBI GmbH
7 | Österfeldtunnel, Horizontalverschiebungen, Vergleich Rechnung – Messung [7]
Credit/Quelle: WBI GmbH
Dieses Beispiel zeigt, dass mit einer wirklichkeitsnahen Erfassung des Festigkeits- und Verformungsverhaltens des Felses nach der AJRM bereits vor vielen Jahren eine wirtschaftliche und sichere Planung möglich war.
In [2, 3] wurde der Österfeldtunnel als Fallbeispiel für einen Vergleich mit einigen der Klassifizierungs-Systeme verwendet. Die unter Annahme der genannten zusätzlichen Horizontalspannung ΔσH = 1 MPa ermittelten Sicherungsempfehlungen nach dem Q-System, RMR-System und RMi-System sind auch in Bild 6 dargestellt. Für jedes System ergibt sich eine andere Sicherungsempfehlung. Vergleichsberechnungen nach der FEM zeigen darüber hinaus, dass der Tunnel mit den nach den genannten Klassifizierungssystemen ermittelten Sicherungsempfehlungen nicht ausreichend standsicher gewesen wäre [2, 3]. Andere Fallbeispiele zeigen, dass die Anwendung der genannten Klassifizierungssysteme im Vergleich zur AJRM-Methode zu deutlich unwirtschaftlicheren Entwürfen geführt hätte (vgl. [2, 3]).
3.2 Buntsandstein, Tunnel Küchen
Der Tunnel Küchen wurde im Zuge der Bundesautobahn A 44 von Kassel nach Eisenach gebaut [9]. Er liegt in der Volpriehausener Wechselfolge des mittleren Buntsandsteins, der im Bereich des Tunnels engständig geschichtet und vertikal geklüftet ist. Im Buntsandstein treten häufig Störungen auf, deren Lage sich in Voruntersuchungen nicht immer genau bestimmen lässt. Auch beim Tunnel Küchen, der als Kalottenvortrieb mit offener Sohle geplant war, wurde eine steil in den Tunnel einfallende Störung angetroffen, die sich im schleifenden Schnitt von einer Seite näherte [10].
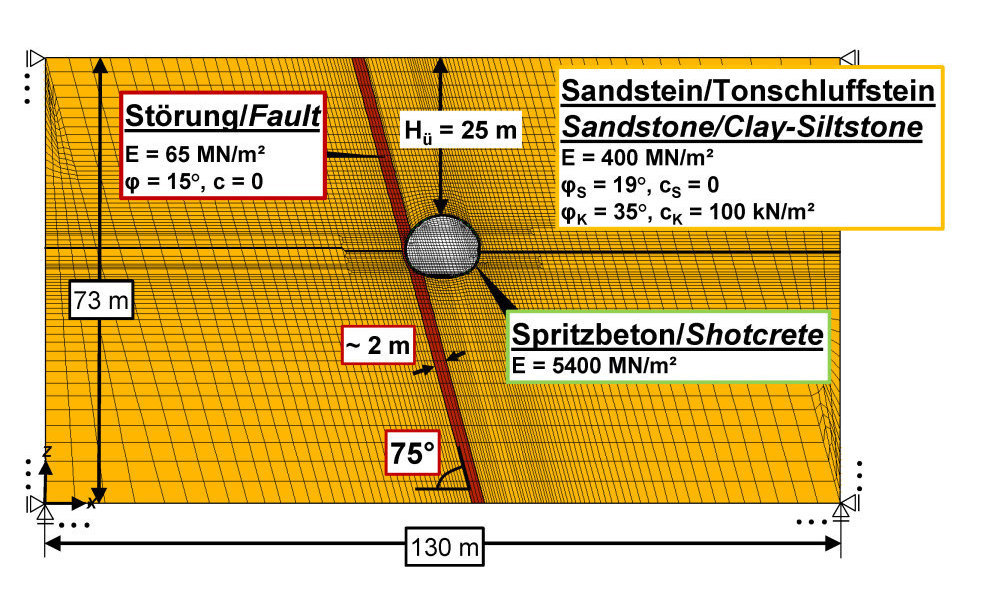 8 | BAB A44, Tunnel Küchen, Störung im schleifenden Schnitt, FE-Netz für Standsicherheitsnachweis [10]
8 | BAB A44, Tunnel Küchen, Störung im schleifenden Schnitt, FE-Netz für Standsicherheitsnachweis [10]
Credit/Quelle: WBI GmbH
8 | BAB A44, Tunnel Küchen, Störung im schleifenden Schnitt, FE-Netz für Standsicherheitsnachweis [10]
Credit/Quelle: WBI GmbH
Mit Hilfe von FE-Berechnungen wurde der Einfluss der Störungszone auf die Standsicherheit des Tunnels für einen Kalottenvortrieb mit offener und geschlossener Sohle untersucht. Bild 8 zeigt das verwendete FE-Netz sowie die Kennwerte. Die Störung wurde diskret nachgebildet. Für den übrigen Bereich des Buntsandsteins war die Anwendung der homogenen Modellvorstellung aufgrund der geringen Trennflächenabstände ausreichend. Das Festigkeits- und Verformungsverhalten der Sand- und Ton-/Schluffsteine des Buntsandsteins wurde nach der AJRM mit dem in Bild 3 dargestellten felsmechanischen Modell erfasst. Die Störungszone wurde, wie erwähnt, diskret nachgebildet. Ihre Kennwerte wurden aus Nachrechnungen ermittelt (Vergleich Rechnung – Messung, siehe [10]).
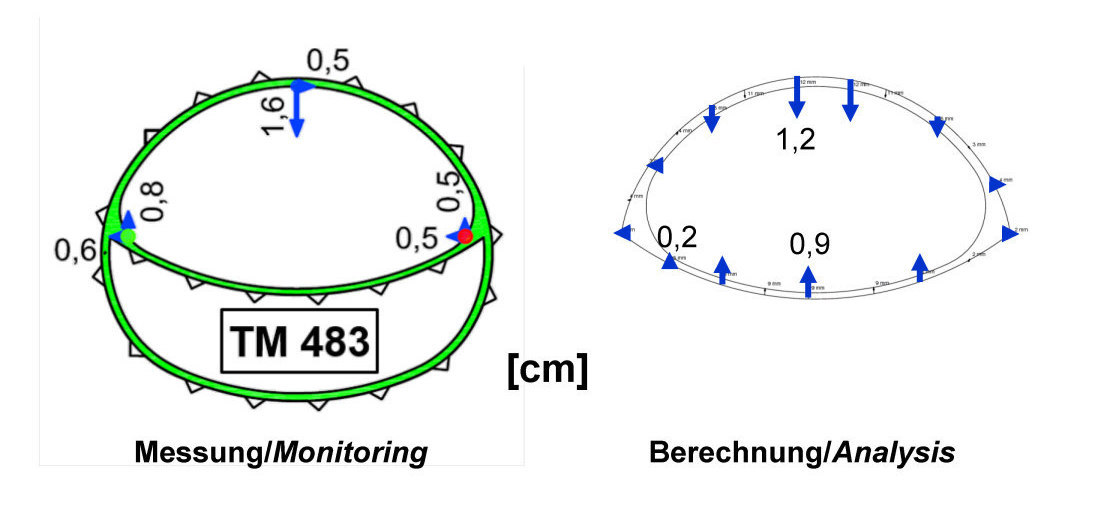 9 | Tunnel Küchen, Kalottenvortrieb mit geschlossener Sohle, Störung außerhalb Einflussbereich, Vergleich Rechnung - Messung
9 | Tunnel Küchen, Kalottenvortrieb mit geschlossener Sohle, Störung außerhalb Einflussbereich, Vergleich Rechnung - Messung
Credit/Quelle: WBI GmbH
9 | Tunnel Küchen, Kalottenvortrieb mit geschlossener Sohle, Störung außerhalb Einflussbereich, Vergleich Rechnung - Messung
Credit/Quelle: WBI GmbH
Bild 9 zeigt den Vergleich von Mess- und Berechnungsergebnissen für einen Kalottenvortrieb mit temporärer Kalottensohle (vgl. Bild 10a). In dem in Bild 9 dargestellten Fall hat die Störungszone einen Abstand von einigen Metern vom Tunnel. Man erkennt, dass die Verschiebungen im Querschnitt nicht von der Störung beeinflusst sind und dass die Ergebnisse der Messungen und Berechnungen in guter Näherung übereinstimmen.
 10a | Tunnel Küchen, Foto Ortsbrust mit temporärer Kalottensohle
10a | Tunnel Küchen, Foto Ortsbrust mit temporärer Kalottensohle
Credit/Quelle: WBI GmbH
10a | Tunnel Küchen, Foto Ortsbrust mit temporärer Kalottensohle
Credit/Quelle: WBI GmbH
 10b | Tunnel Trimberg, Foto Ortsbrust im Buntsandstein [10]
10b | Tunnel Trimberg, Foto Ortsbrust im Buntsandstein [10]
Credit/Quelle: WBI GmbH
10b | Tunnel Trimberg, Foto Ortsbrust im Buntsandstein [10]
Credit/Quelle: WBI GmbH
Wenn die Störung jedoch in die Nähe des Tunnels kommt oder diesen schneidet, dann werden die Verschiebungen vor allem auf der Seite der Störung deutlich größer. Mit einem Kalottenvortrieb mit geschlossener Sohle lassen sich die Verschiebungen beherrschen (Bild 11, rechts), wohingegen sich bei einem Kalottenvortrieb mit offener Sohle die Standsicherheit im von der Störung betroffenen Ulmenbereich nicht gewährleisten lässt (Bild 11, links). Dies haben auch Beobachtungen vor Ort gezeigt.
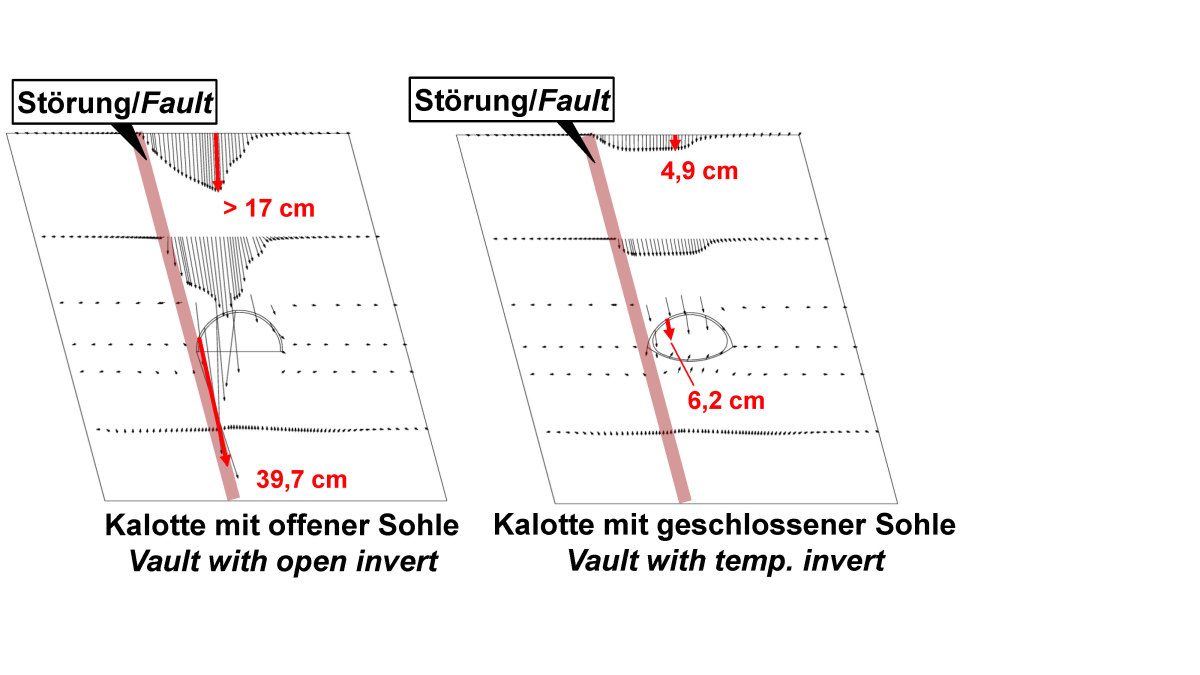 11 | Tunnel Küchen, Störungszone im Querschnittsbereich, Verschiebungen für einen Kalottenvortrieb mit offener und geschlossener Sohle [10]
11 | Tunnel Küchen, Störungszone im Querschnittsbereich, Verschiebungen für einen Kalottenvortrieb mit offener und geschlossener Sohle [10]
Credit/Quelle: [10]
11 | Tunnel Küchen, Störungszone im Querschnittsbereich, Verschiebungen für einen Kalottenvortrieb mit offener und geschlossener Sohle [10]
Credit/Quelle: [10]
Dieses Beispiel zeigt sehr klar, dass es für einen sicheren Entwurf essentiell ist, die Anisotropie der Festigkeit und Verformbarkeit, die sich z. B. aus Wechsellagerungen, Trennflächen und auch Störungszonen ergibt, wirklichkeitsnah zu erfassen und zu berücksichtigen. Es wird ebenso deutlich, dass dies mit der AJRM möglich ist. Der Aufwand für entsprechende Berechnungen ist heutzutage nicht mehr als Hinderungsgrund für die Anwendung zu sehen.
 12 | NBS Hannover–Würzburg, Einschnitt Überholbahnhof Körle,
12 | NBS Hannover–Würzburg, Einschnitt Überholbahnhof Körle,
Böschung im Buntsandstein
Credit/Quelle: WBI GmbH
12 | NBS Hannover–Würzburg, Einschnitt Überholbahnhof Körle,
Böschung im Buntsandstein
Credit/Quelle: WBI GmbH
Ein weiteres Beispiel aus dem Buntsandstein ist in Bild 12 dargestellt. Es liegt zwar schon einige Jahre zurück, ist aber auch für die in jüngster Zeit errichteten und in naher Zukunft zu errichtenden Bauwerke im Buntsandstein von Relevanz. Für die Eisenbahnneubaustrecke zwischen Kassel und Fulda wurden zahlreiche Einschnitte im Buntsandstein hergestellt. Aufgrund der geringen Scherfestigkeit auf den bankungsparallelen Schichtfugen des Buntsandsteins (Reibungswinkel φB ~ 8–20°, cB ~ 0) und des Einfallwinkels der Trennflächen mussten die Böschungen trotz der flachen Neigung von nur 30° umfangreich mit Vorspannankern gesichert werden. Ohne diese Sicherung kam es zum Versagen entlang der Trennflächen (Bild 12). Dies wird jedoch nur dann zutreffend erkannt, wenn die Festigkeitsanisotropie des Buntsandsteins entsprechend berücksichtigt wird.
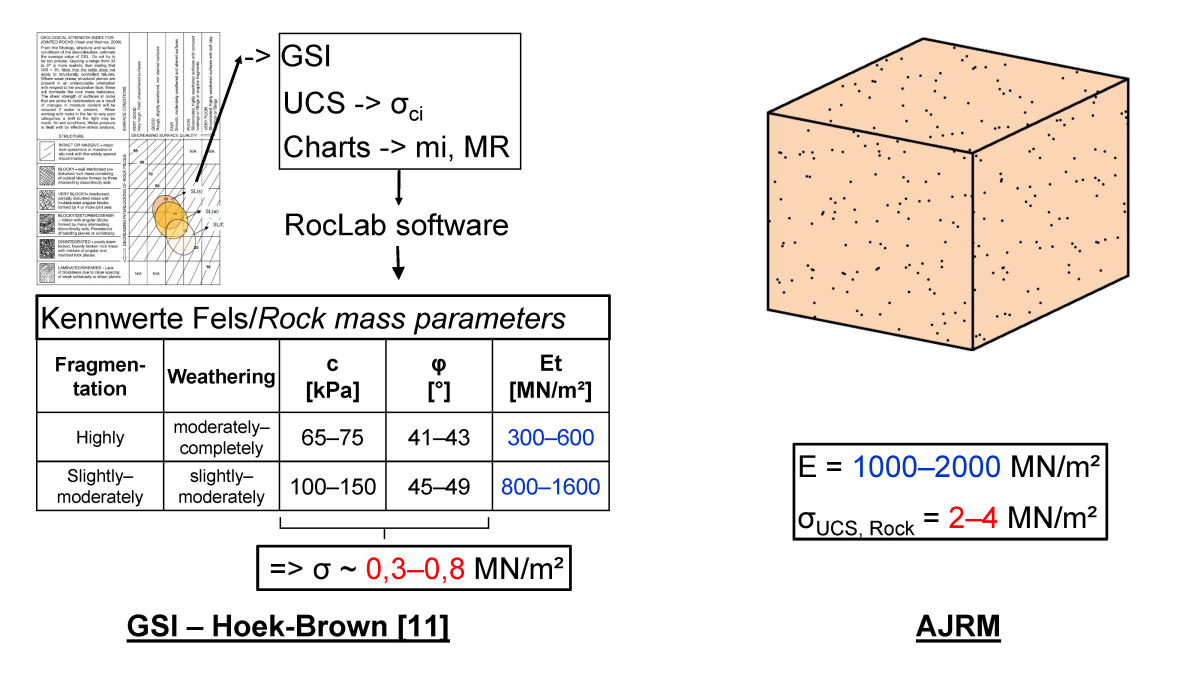 13 | Green Line, Katar, Simsima Kalkstein, Kennwerte nach Hoek-Brown [11] im Vergleich zu AJRM [13, 14]
13 | Green Line, Katar, Simsima Kalkstein, Kennwerte nach Hoek-Brown [11] im Vergleich zu AJRM [13, 14]
Credit/Quelle: Bild oben links -> [11]. Rest: WBI GmbH
13 | Green Line, Katar, Simsima Kalkstein, Kennwerte nach Hoek-Brown [11] im Vergleich zu AJRM [13, 14]
Credit/Quelle: Bild oben links -> [11]. Rest: WBI GmbH
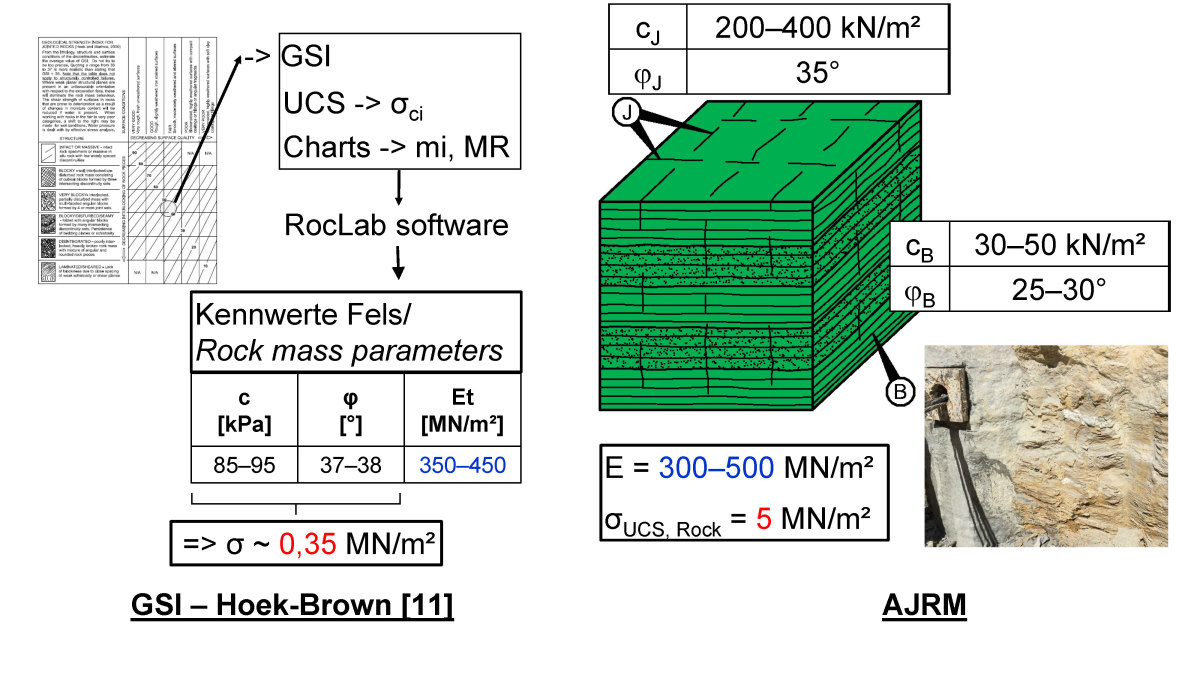 14 | Green Line, Katar, Midra Shale, Kennwerte nach Hoek-Brown [11] im Vergleich zu AJRM [13, 14]
14 | Green Line, Katar, Midra Shale, Kennwerte nach Hoek-Brown [11] im Vergleich zu AJRM [13, 14]
Credit/Quelle: [11]; WBI GmbH
14 | Green Line, Katar, Midra Shale, Kennwerte nach Hoek-Brown [11] im Vergleich zu AJRM [13, 14]
Credit/Quelle: [11]; WBI GmbH
3.3 Kalkstein, Green Line, Katar
Für die Stationen der U-Bahn-Linie Green Line in Katar wurden zahlreiche Baugruben im tertiären Kalkstein gebaut. Die Kennwerte des Felses wurden vom Planer auf Grundlage des Hoek-Brown Bruchkriteriums ermittelt [11]. Auf Grundlage der Erkundungsergebnisse und eigener Einschätzung sowie unter Zuhilfenahme der Grafiken von Hoek-Brown hat der Planer die GSI-Werte, die Gesteinsfestigkeiten (σci) sowie die Konstante mi und den Verhältniswert MR ermittelt. Auf dieser Grundlage hat er mit der RocLab Software [12] die Kennwerte des Felses, Kohäsion, Reibungswinkel und Verformungsmodul, bestimmt. Beispielhaft sind die Ergebnisse für zwei wesentliche Schichtglieder, den Simsima Limestone und den Midra Shale, auf Bild 13 und Bild 14 jeweils links dargestellt. Der Fels wird wie ein homogenes, isotropes Material betrachtet. Dabei werden vergleichsweise geringe isotrope Festigkeiten angegeben, die insbesondere im Falle des Midra Shale in der Größenordnung der Scherfestigkeit der in diesem Fall näherungsweise horizontalen, schichtparallelen Trennflächen liegen. Auf dieser Grundlage und unter Ansatz der relevanten Lasten wurde die Baugrubensicherung geplant. Wegen der geringen angenommenen Festigkeiten ergab sich eine Sicherung mit einer aufgelösten Bohrpfahlwand. Die Bohrpfähle, die einem Durchmesser von 1 m besaßen wurden alle 2,5 m bis 4 m mit 15 bis 25,5 m langen Vorspannankern rückverankert (vgl. Bild 15, links).
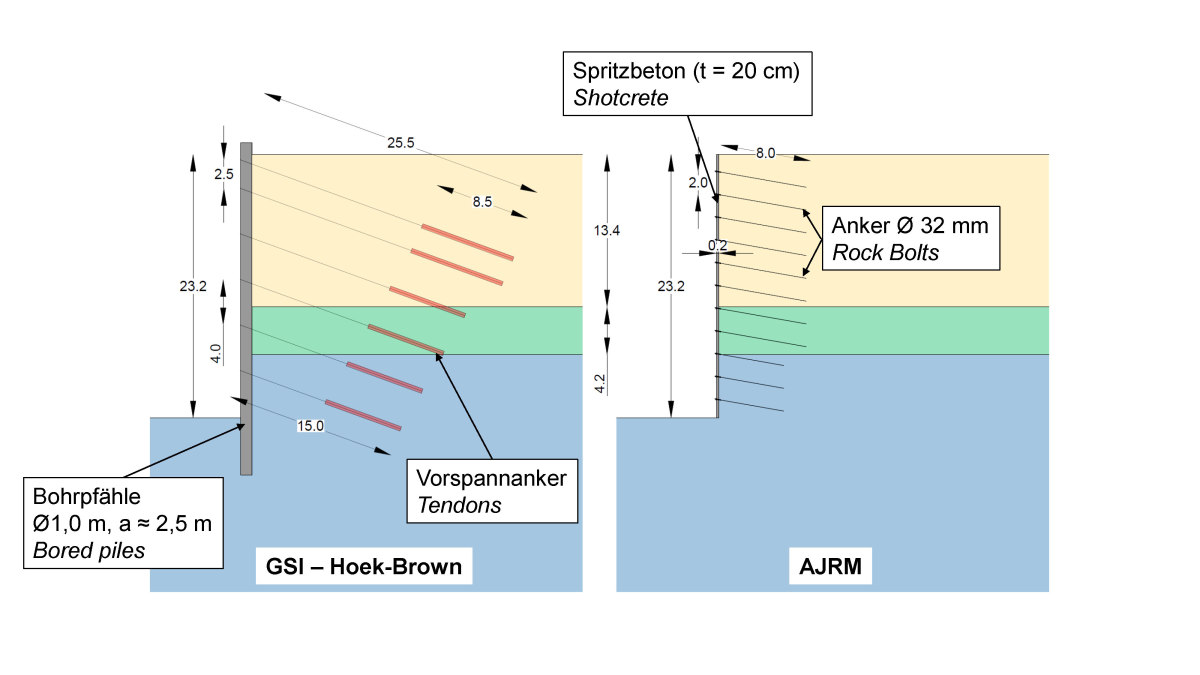 15 | Green Line, Katar, Baugrubensicherung auf Basis von Kennwerten nach Hoek-Brown [11] im Vergleich zu AJRM [10]
15 | Green Line, Katar, Baugrubensicherung auf Basis von Kennwerten nach Hoek-Brown [11] im Vergleich zu AJRM [10]
Credit/Quelle: [10]
15 | Green Line, Katar, Baugrubensicherung auf Basis von Kennwerten nach Hoek-Brown [11] im Vergleich zu AJRM [10]
Credit/Quelle: [10]
Auf Bitte der ausführenden Unternehmung haben die Autoren eigene Betrachtungen unter Ansatz des AJRM durchgeführt. Eine Begehung vor Ort sowie das Studium der Ergebnisse der Erkundungen ergab, dass es sich beim Simsima Limestone, in dem etwa die oberen zwei Drittel der betrachteten Baugrube liegen (Bild 15), um einen feinkörnigen kristallinen Kalkstein nahezu ohne Klüfte und Bankungsfugen handelt. Er ist homogen und isotrop hinsichtlich Festigkeit und Verformbarkeit. Die felsmechanischen Kennwerte wurden wie in Bild 13 rechts dargestellt eingeschätzt. Insbesondere die Festigkeit ist deutlich höher als nach Hoek-Brown vom Planer ermittelt (Bild 13, links).
Der unterhalb des Simsima Limestones anstehende Midra Shale weist eine ausgeprägte, teilweise engständige horizontale Schichtung auf (Foto in Bild 14). Darüber hinaus sind steil stehende Klüfte zu beobachten. Nach dem AJRM wird diese Anisotropie in der Festigkeit berücksichtigt, indem einerseits die Festigkeit des Gesteins und andererseits reduzierte Scherfestigkeiten auf den Trennflächen berücksichtigt werden (vgl. Bild 14, rechts). Es wurde von einer isotropen Verformbarkeit im elastischen Bereich ausgegangen. Der Verformungsmodul liegt bei beiden Ansätzen in einer ähnlichen Größenordnung. Der Vergleich der Festigkeitskennwerte nach AJRM mit den Festigkeitskennwerten, die mit den Ansätzen des Planers auf der Grundlage von Hoek-Brown ermittelt wurden, zeigt jedoch sehr deutliche Unterschiede. Der Fels wurde, wie bereits erwähnt, nach Hoek-Brown homogen-isotrop betrachtet. Dabei wurden für den Fels Festigkeiten angegeben, die in der Größenordnung der Scherfestigkeit der schichtparallelen Trennflächen liegen. Der Fels wurde damit annähernd wie ein Boden betrachtet. Dies trägt den tatsächlichen Verhältnissen nicht Rechnung und führt insbesondere bei der hier vorliegenden horizontalen Schichtung zu einer deutlichen Überdimensionierung der Sicherungsmaßnahmen.
Für das unterste Schichtglied, das hier nicht näher betrachtet werden soll, fällt der Vergleich ähnlich aus wie für den Midra Shale.
Mit den nach AJRM auf der Grundlage der Erkundungen und der Erfahrung der Autoren ermittelten Kennwerten konnte die Standsicherheit der Baugrube bei gleichen Lastannahmen mit einer deutlich geringeren Baugrubensicherung mit 20 cm Spritzbeton und bis zu 8 m langen, schlaffen Ankern, die in einem Raster von 2 m x 3 m angeordnet werden, nachgewiesen werden (Bild 15, rechts). Die wirklichkeitsnahe Erfassung der Festigkeits- und Verformungseigenschaften des Felses erlaubte also in diesem Fall eine erheblich wirtschaftlichere Planung und Bauausführung. Leider konnte diese vor Ort nur noch teilweise umgesetzt werden, da ein Großteil der Bohrpfähle bereits ausgeführt worden war.
4 Ausblick auf Teil 2
Die Darstellung der Fallbeispiele zeigt sehr deutlich, dass die wirklichkeitsnahe Erfassung der Verformbarkeit und Festigkeit des Felses mit dem AJRM einen sicheren und wirtschaftlichen Entwurf ermöglicht. Dies kann auch anhand baubegleitender Messungen bestätigt werden.
Im Teil 2 des Artikels wird das zum AJRM gehörige felshydraulische Modell mit ausgewählten Fallbeispielen vorgestellt. Zudem wird auf die Methoden zur Ermittlung der felsmechanischen und felshydraulischen Kennwerte eingegangen.
References/Literatur
[1] Abbas, S.M.; Konietzky, H.: Rock mass classification systems. Chapter 10 of E-Book “Introduction into geomechanics”.
[2] Sommer, R.: Kritische Wertung der Methoden der Gebirgsklassifizierung im Tunnelbau. Geotechnik in Forschung und Praxis,
WBI-PRINT 16, VGE: Essen, 2009.
[3] Wittke W., Sommer, R.: Designs in jointed rock. World Tunneling July/August 2011, pp. 30 to 34.
Corresponding discussion: + Barton, N.: A measured response. World Tunneling September 2011, pp. 13 to 17.
+ Wittke, W.; Sommer, R.: Answer to the “measured response”. World Tunneling, 6.10.2011.
[4] Hoek, E.; Carranza-Torres, C.; Corkum, B.: Hoek-Brown Failure Criterion – 2002 Edition. In: Hammah, R.; Bawden, W.; Curran,
J. and Telesnicki, M., eds., Mining and Tunneling Innovation and Opportunity.
[5] Wittke, W.: Felsmechanik, Grundlagen für wirtschaftliches Bauen im Fels. Springer-Verlag, Berlin 1984. ISBN-Nr.: 3-540-13016-0 /
0-387-13016-0.
English Version: Wittke, W.: Rock mechanics – Theory and application with case histories. Springer: Berlin, Heidelberg, New York,
Tokyo, 1990. ISBN-Nr.: 3-540-52719-2 / 0-387-52719-2
[6] Wittke, W.: Rock Mechanics based on an Anisotropic Jointed Rock Model (AJRM), Verlag Ernst & Sohn GmbH & Co. KG, Berlin 2014.
ISBN-Nr.: 978-3-433-03079-0.
[7] Wittke, W.; Pierau, B.; Erichsen, C.: Statik und Konstruktion der Spritzbetonbauweise. Geotechnik in Forschung und Praxis, WBI-Print 5,
Verlag Glückauf GmbH, Essen, 2002. ISBN-Nr.: 3-7739-1305-2.
English version: New Austrian Tunneling Method (NATM) – Stability Analyses and Design. Available for download in WBI-Library on
[8] Wittke, W.; Wittke, M.; Druffel, R.; Rath, A.; Osthoff, G.: Großquerschnitte im Anfahrbereich Hauptbahnhof Süd,
Statische Berechnungen, Senkungsprognosen und Baubetriebliche Aspekte. Vortrag anlässlich des 5. Felsmechanik- und
Tunnelbautages im WBI-Center am 23.05.2019. WBI-Print 22, Weinheim, 2019. ISBN-Nr.: 978-3-00-063255-6.
[9]
https://mobil.hessen.de/a44 mobil.hessen.de: A44 Kassel – Herleshausen (abgerufen am 22.10.2019, 13.22 Uhr).
[10] Wittke, W.; Wittke-Schmitt, B.; Wittke-Gattermann, P.: Das Modell AJRM als Grundlage für wirtschaftliches und sicheres Planen und
Bauen im klüftigen Fels. Vortrag anlässlich des 5. Felsmechanik- und Tunnelbautages im WBI-Center am 23.05.2019. WBI-Print 22,
Weinheim, 2019. ISBN-Nr.: 978-3-00-063255-6
[11] Green Line in Katar: Baugrube Station Education City South East. Projektunterlagen von anderen Projektbeteiligten (Planer), 2014.
Unveröffentlicht.
[12]
www.rocscience.com/documents/pdfs/uploads/8079.pdf: RocLab 1.0 Rock Mass strength analysis using the generalized Hoek-Brown
failure criterion. (Abgerufen am 27.04.2021, 11.25 Uhr)
[13] Wittke-Schmitt, B.; Küpper, H.-J.; Wenkenbach, H.: Green Line in Qatar, bergmännische Unterfahrung einer 8spurigen Straße in
Doha. Vortrag anlässlich des 3. Felsmechanik- und Tunnelbau-Tags im WBI-Center am 11.05.2017. WBI-PRINT 20, Weinheim, 2017.
ISBN-NR.: 978-3-00-057227-2
[14] Wenkenbach, H.; Wittke, M.; Wittke-Schmitt, B.; Küpper, H.-J.: Green Line Katar: Konventionelle Tunnelvortriebe, Planung und
Ausführung auf der Grundlage der AJRM-Methode. Veröffentlichung in der Zeitschrift „Tunnel“, Jahrgang 37, 05/2018, S. 16 bis 26, Bauverlag BV GmbH, Gütersloh

 1 | Lias α – Foto Ortsbrust, Gefügemodell und elastische Konstanten als Teil eines felsmechanischen Modells
1 | Lias α – Foto Ortsbrust, Gefügemodell und elastische Konstanten als Teil eines felsmechanischen Modells  2 | Fels mit 1 Schar durchgehender, gefüllter Trennflächen – Foto und Bestimmung der elastischen Konstanten [6]
2 | Fels mit 1 Schar durchgehender, gefüllter Trennflächen – Foto und Bestimmung der elastischen Konstanten [6]  3 | Buntsandstein – Foto Ortsbrust, Gefügemodell und Festigkeitseigenschaften als Teil des felsmechanischen Modells
3 | Buntsandstein – Foto Ortsbrust, Gefügemodell und Festigkeitseigenschaften als Teil des felsmechanischen Modells  4 | Trennflächenabstand im Vergleich zu Bauwerksab-
4 | Trennflächenabstand im Vergleich zu Bauwerksab- 5 | Ortsumfahrung Vaihingen (Stuttgart), Österfeldtunnel, Geologischer Längsschnitt [7]
5 | Ortsumfahrung Vaihingen (Stuttgart), Österfeldtunnel, Geologischer Längsschnitt [7]  6 | Österfeldtunnel, Ausbruch und Sicherung auf Basis AJRM im Vergleich mit Sicherungsempfehlungen nach Klassifizierungssystemen Q, RMR und RMi [2, 3]
6 | Österfeldtunnel, Ausbruch und Sicherung auf Basis AJRM im Vergleich mit Sicherungsempfehlungen nach Klassifizierungssystemen Q, RMR und RMi [2, 3]  7 | Österfeldtunnel, Horizontalverschiebungen, Vergleich Rechnung – Messung [7]
7 | Österfeldtunnel, Horizontalverschiebungen, Vergleich Rechnung – Messung [7]  8 | BAB A44, Tunnel Küchen, Störung im schleifenden Schnitt, FE-Netz für Standsicherheitsnachweis [10]
8 | BAB A44, Tunnel Küchen, Störung im schleifenden Schnitt, FE-Netz für Standsicherheitsnachweis [10]  9 | Tunnel Küchen, Kalottenvortrieb mit geschlossener Sohle, Störung außerhalb Einflussbereich, Vergleich Rechnung - Messung
9 | Tunnel Küchen, Kalottenvortrieb mit geschlossener Sohle, Störung außerhalb Einflussbereich, Vergleich Rechnung - Messung  11 | Tunnel Küchen, Störungszone im Querschnittsbereich, Verschiebungen für einen Kalottenvortrieb mit offener und geschlossener Sohle [10]
11 | Tunnel Küchen, Störungszone im Querschnittsbereich, Verschiebungen für einen Kalottenvortrieb mit offener und geschlossener Sohle [10]  12 | NBS Hannover–Würzburg, Einschnitt Überholbahnhof Körle,
12 | NBS Hannover–Würzburg, Einschnitt Überholbahnhof Körle,  13 | Green Line, Katar, Simsima Kalkstein, Kennwerte nach Hoek-Brown [11] im Vergleich zu AJRM [13, 14]
13 | Green Line, Katar, Simsima Kalkstein, Kennwerte nach Hoek-Brown [11] im Vergleich zu AJRM [13, 14]  14 | Green Line, Katar, Midra Shale, Kennwerte nach Hoek-Brown [11] im Vergleich zu AJRM [13, 14]
14 | Green Line, Katar, Midra Shale, Kennwerte nach Hoek-Brown [11] im Vergleich zu AJRM [13, 14]  15 | Green Line, Katar, Baugrubensicherung auf Basis von Kennwerten nach Hoek-Brown [11] im Vergleich zu AJRM [10]
15 | Green Line, Katar, Baugrubensicherung auf Basis von Kennwerten nach Hoek-Brown [11] im Vergleich zu AJRM [10]